15
апр
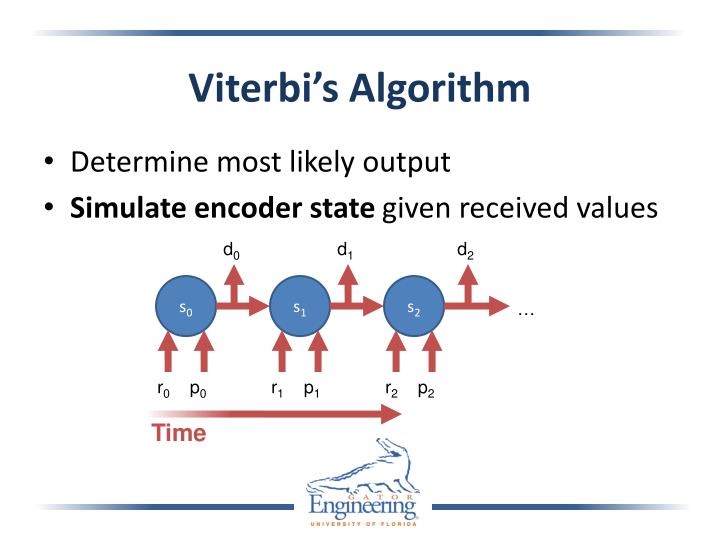
The Viterbi algorithm (VA) is appropriate. This article will attempt to explain why, by briefly recounting the history of the VA. It is a “personal history,” because the story of the VA is so intertwined with my own history that I can recount much of it from a personal perspective. 2 Invention of the Viterbi algorithm. Viterbi Algorithm Ppt For Mac. Viterbi Algorithm Complexity; Viterbi Algorithm Example. EVALUATION– given observation O=(o1, o2,oT ) and model, efficiently.
A Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has beenencoded using a convolutional code or trellis code.
There are other algorithms for decoding a convolutionally encoded stream (for example, the Fano algorithm). The Viterbi algorithm is the most resource-consuming, but it does the maximum likelihood decoding. It is most often used for decoding convolutional codes with constraint lengths k≤3, but values up to k=15 are used in practice.
Viterbi decoding was developed by Andrew J. Viterbi and published in the paper Viterbi, A. (April 1967). 'Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm'. IEEE Transactions on Information Theory. 13 (2): 260–269. doi:10.1109/tit.1967.1054010.
There are both hardware (in modems) and software implementations of a Viterbi decoder.
Viterbi decoding is used in the iterative Viterbi decoding algorithm.
Hardware implementation[edit]
A hardware Viterbi decoder for basic (not punctured) code usually consists of the following major blocks:
- Branch metric unit (BMU)
- Path metric unit (PMU)
- Traceback unit (TBU)
Branch metric unit (BMU)[edit]
A branch metric unit's function is to calculate branch metrics, which are normed distances between every possible symbol in the code alphabet, and the received symbol.
There are hard decision and soft decision Viterbi decoders. A hard decision Viterbi decoder receives a simple bitstream on its input, and a Hamming distance is used as a metric. A soft decision Viterbi decoder receives a bitstream containing information about the reliability of each received symbol. For instance, in a 3-bit encoding, this reliability information can be encoded as follows:
MorphVOX Pro Serial Key contains different languages like English and Spanish, according to user requirements. It includes a big library of free sounds. This software contains less range of frequencies that perform quality sound operations. There is a complete combination of music for user’s gossip programs. MorphVOX Pro Crack Features. Download the MorphVOX Crack from here. Get the Trial Version of MorphoVOX from the link below and install it. Run the program. Move the Crack into the installation folder. Click on it and wait for the activation process. You can use the Serial key also for activation that is available in a readme file. MorphVOX Pro has a 10-band equalizer. This way you can add sound effects and match them perfectly to your voice with a little practice. For Playing radio at your different devices try ProgDVB Pro Crack. When you run MorphVOX Pro License Key for the first time, a wizard will help you get started by adjusting the sound and your microphone. The vocal range of MorphVOX Pro is very versatile and offers an advantage over many competitors. Morphvox pro download. MorphVOX Pro Key gives you to access a Pro version from the free trial version with limited functionality. So, MorphVOX Pro 4.4.78 Build 23625 Key has many features like background music while talking with your friend.
meaning| 000 | strongest | 0 |
| 001 | relatively strong | 0 |
| 010 | relatively weak | 0 |
| 011 | weakest | 0 |
| 100 | weakest | 1 |
| 101 | relatively weak | 1 |
| 110 | relatively strong | 1 |
| 111 | strongest | 1 |
Of course, it is not the only way to encode reliability data.
The squaredEuclidean distance is used as a metric for soft decision decoders.
Path metric unit (PMU)[edit]
A path metric unit summarizes branch metrics to get metrics for paths, where K is the constraint length of the code, one of which can eventually be chosen as optimal. Every clock it makes decisions, throwing off wittingly nonoptimal paths. The results of these decisions are written to the memory of a traceback unit.
The core elements of a PMU are ACS (Add-Compare-Select) units. The way in which they are connected between themselves is defined by a specific code's trellis diagram.
Since branch metrics are always , there must be an additional circuit (not shown on the image) preventing metric counters from overflow. An alternate method that eliminates the need to monitor the path metric growth is to allow the path metrics to 'roll over'; to use this method it is necessary to make sure the path metric accumulators contain enough bits to prevent the 'best' and 'worst' values from coming within 2(n-1) of each other. The compare circuit is essentially unchanged.
It is possible to monitor the noise level on the incoming bit stream by monitoring the rate of growth of the 'best' path metric. A simpler way to do this is to monitor a single location or 'state' and watch it pass 'upward' through say four discrete levels within the range of the accumulator. As it passes upward through each of these thresholds, a counter is incremented that reflects the 'noise' present on the incoming signal.
Traceback unit (TBU)[edit]
Back-trace unit restores an (almost) maximum-likelihood path from the decisions made by PMU. Since it does it in inverse direction, a viterbi decoder comprises a FILO (first-in-last-out) buffer to reconstruct a correct order.
Note that the implementation shown on the image requires double frequency. There are some tricks that eliminate this requirement.
Implementation issues[edit]
Quantization for soft decision decoding[edit]
In order to fully exploit benefits of soft decision decoding, one needs to quantize the input signal properly. The optimal quantization zone width is defined by the following formula:
where is a noise power spectral density, and k is a number of bits for soft decision.
Euclidean metric computation[edit]
The squared norm () distance between the received and the actual symbols in the code alphabet may be further simplified into a linear sum/difference form, which makes it less computationally intensive.
Consider a 1/2 convolutional coder, which generates 2 bits (00, 01, 10 or 11) for every input bit (1 or 0). These Return-to-Zero signals are translated into a Non-Return-to-Zero form shown alongside.
Each square term is a normed distance, depicting the energy of the symbol. For ex., the energy of the symbol vi = {±1, ±1} may be computed as
Thus, the energy term of all symbols in the code alphabet is constant (at (normalized) value 2).
The Add-Compare-Select (ACS) operation compares the metric distance between the received symbol vr and any 2 symbols in the code alphabet whose paths merge at a node in the corresponding trellis, vi(0) and vi(1). This is equivalent to comparing
and
But, from above we know that the energy of vi is constant (equal to (normalized) value of 2), and the energy of vr is the same in both cases. This reduces the comparison to a minima function between the 2 (middle) dot product terms,
since a min operation on negative numbers may be interpreted as an equivalent max operation on positive quantities.
Each dot product term may be expanded as
where, the signs of each term depend on symbols, vi(0) and vi(1), being compared. Thus, the squared Euclidean metric distance calculation to compute the branch metric may be performed with a simple add/subtract operation.
Traceback[edit]
The general approach to traceback is to accumulate path metrics for up to five times the constraint length (5 (K - 1)), find the node with the largest accumulated cost, and begin traceback from this node.
However, computing the node which has accumulated the largest cost (either the largest or smallest integral path metric) involves finding the maxima or minima of several (usually 2K-1) numbers, which may be time consuming when implemented on embedded hardware systems.
Most communication systems employ Viterbi decoding involving data packets of fixed sizes, with a fixed bit/byte pattern either at the beginning or/and at the end of the data packet. By using the known bit/byte pattern as reference, the start node may be set to a fixed value, thereby obtaining a perfect Maximum Likelihood Path during traceback.
Limitations[edit]
A physical implementation of a viterbi decoder will not yield an exact maximum-likelihood stream due to quantization of the input signal, branch and path metrics, and finite traceback length. Practical implementations do approach within 1dB of the ideal.
The output of a Viterbi decoder, when decoding a message damaged by an additive gaussian channel, has errors grouped in error bursts.[1][2]Single-error-correcting codes alone can't correct such bursts, so either the convolutional code and the Viterbi decoder must be designed powerful enough to drive down errors to an acceptable rate, or burst error-correcting codes must be used.

Punctured codes[edit]
A hardware viterbi decoder of punctured codes is commonly implemented in such a way:
- A depuncturer, which transforms the input stream into the stream which looks like an original (non punctured) stream with ERASE marks at the places where bits were erased.
- A basic viterbi decoder understanding these ERASE marks (that is, not using them for branch metric calculation).
Software implementation[edit]
One of the most time-consuming operations is an ACS butterfly, which is usually implemented using an assembly language and appropriate instruction set extensions (such as SSE2) to speed up the decoding time.
Applications[edit]
The Viterbi decoding algorithm is widely used in the following areas:
- Radio communication: digital TV (ATSC, QAM, DVB-T, etc.), radio relay, satellite communications, PSK31 digital mode for amateur radio.
- Decoding trellis-coded modulation (TCM), the technique used in telephone-line modems to squeeze high spectral efficiency out of 3 kHz-bandwidth analog telephone lines.
- Computer storage devices such as hard disk drives.
References[edit]
- ^Stefan Host, Rolf Johannesson, Dmitrij K. Zigangirod, Kamil Sh. Zigangirod, and Viktor V. Zyablod.'On the Distribution of the Output Error Burst Lengths for Viterbi Decoding of Convolutional Codes'.
- ^Curry, S. J.; Harmon, W. D.'A bound on Viterbi decoder error burst length'.
External links[edit]
| Wikimedia Commons has media related to Viterbi coding. |
- Forney, G. David, Jr (29 Apr 2005). 'The Viterbi Algorithm: A Personal History'. arXiv:cs/0504020.
- Details on Viterbi decoding, as well as a bibliography.
- Viterbi algorithm explanation with the focus on hardware implementation issues.
- r=1/6 k=15 coding for the Cassini mission to Saturn.
- Online Generator of optimized software Viterbi decoders (GPL).
- GPL Viterbi decoder software for four standard codes.
- Description of a k=24 Viterbi decoder, believed to be the largest ever in practical use.
- Generic Viterbi decoder hardware (GPL).
Popular Posts
- meaning000strongest0001relatively strong0010relatively weak0011weakest0100weakest1101relatively weak1110relatively strong1111strongest1
Of course, it is not the only way to encode reliability data.
The squaredEuclidean distance is used as a metric for soft decision decoders.
Path metric unit (PMU)[edit]
A sample implementation of a path metric unit for a specific K=4 decoderA path metric unit summarizes branch metrics to get metrics for paths, where K is the constraint length of the code, one of which can eventually be chosen as optimal. Every clock it makes decisions, throwing off wittingly nonoptimal paths. The results of these decisions are written to the memory of a traceback unit.
The core elements of a PMU are ACS (Add-Compare-Select) units. The way in which they are connected between themselves is defined by a specific code's trellis diagram.
Since branch metrics are always , there must be an additional circuit (not shown on the image) preventing metric counters from overflow. An alternate method that eliminates the need to monitor the path metric growth is to allow the path metrics to 'roll over'; to use this method it is necessary to make sure the path metric accumulators contain enough bits to prevent the 'best' and 'worst' values from coming within 2(n-1) of each other. The compare circuit is essentially unchanged.
A sample implementation of an ACS unitIt is possible to monitor the noise level on the incoming bit stream by monitoring the rate of growth of the 'best' path metric. A simpler way to do this is to monitor a single location or 'state' and watch it pass 'upward' through say four discrete levels within the range of the accumulator. As it passes upward through each of these thresholds, a counter is incremented that reflects the 'noise' present on the incoming signal.
Traceback unit (TBU)[edit]
A sample implementation of a traceback unitBack-trace unit restores an (almost) maximum-likelihood path from the decisions made by PMU. Since it does it in inverse direction, a viterbi decoder comprises a FILO (first-in-last-out) buffer to reconstruct a correct order.
Note that the implementation shown on the image requires double frequency. There are some tricks that eliminate this requirement.
Implementation issues[edit]
Quantization for soft decision decoding[edit]
In order to fully exploit benefits of soft decision decoding, one needs to quantize the input signal properly. The optimal quantization zone width is defined by the following formula:
where is a noise power spectral density, and k is a number of bits for soft decision.
Euclidean metric computation[edit]
The squared norm () distance between the received and the actual symbols in the code alphabet may be further simplified into a linear sum/difference form, which makes it less computationally intensive.
Consider a 1/2 convolutional coder, which generates 2 bits (00, 01, 10 or 11) for every input bit (1 or 0). These Return-to-Zero signals are translated into a Non-Return-to-Zero form shown alongside.

D = ( v r → − v i → ) 2 = v r → 2 − 2 v r → v i → + v i → 2 Each square term is a normed distance, depicting the energy of the symbol. For ex., the energy of the symbol vi = {±1, ±1} may be computed as
Thus, the energy term of all symbols in the code alphabet is constant (at (normalized) value 2).
The Add-Compare-Select (ACS) operation compares the metric distance between the received symbol vr and any 2 symbols in the code alphabet whose paths merge at a node in the corresponding trellis, vi(0) and vi(1). This is equivalent to comparing
and
But, from above we know that the energy of vi is constant (equal to (normalized) value of 2), and the energy of vr is the same in both cases. This reduces the comparison to a minima function between the 2 (middle) dot product terms,
since a min operation on negative numbers may be interpreted as an equivalent max operation on positive quantities.
Each dot product term may be expanded as
where, the signs of each term depend on symbols, vi(0) and vi(1), being compared. Thus, the squared Euclidean metric distance calculation to compute the branch metric may be performed with a simple add/subtract operation.
Traceback[edit]
The general approach to traceback is to accumulate path metrics for up to five times the constraint length (5 (K - 1)), find the node with the largest accumulated cost, and begin traceback from this node.
However, computing the node which has accumulated the largest cost (either the largest or smallest integral path metric) involves finding the maxima or minima of several (usually 2K-1) numbers, which may be time consuming when implemented on embedded hardware systems.
Most communication systems employ Viterbi decoding involving data packets of fixed sizes, with a fixed bit/byte pattern either at the beginning or/and at the end of the data packet. By using the known bit/byte pattern as reference, the start node may be set to a fixed value, thereby obtaining a perfect Maximum Likelihood Path during traceback.
Limitations[edit]
A physical implementation of a viterbi decoder will not yield an exact maximum-likelihood stream due to quantization of the input signal, branch and path metrics, and finite traceback length. Practical implementations do approach within 1dB of the ideal.
The output of a Viterbi decoder, when decoding a message damaged by an additive gaussian channel, has errors grouped in error bursts.[1][2]Single-error-correcting codes alone can't correct such bursts, so either the convolutional code and the Viterbi decoder must be designed powerful enough to drive down errors to an acceptable rate, or burst error-correcting codes must be used.

Punctured codes[edit]
A hardware viterbi decoder of punctured codes is commonly implemented in such a way:
- A depuncturer, which transforms the input stream into the stream which looks like an original (non punctured) stream with ERASE marks at the places where bits were erased.
- A basic viterbi decoder understanding these ERASE marks (that is, not using them for branch metric calculation).
Software implementation[edit]
One of the most time-consuming operations is an ACS butterfly, which is usually implemented using an assembly language and appropriate instruction set extensions (such as SSE2) to speed up the decoding time.
Applications[edit]
The Viterbi decoding algorithm is widely used in the following areas:
- Radio communication: digital TV (ATSC, QAM, DVB-T, etc.), radio relay, satellite communications, PSK31 digital mode for amateur radio.
- Decoding trellis-coded modulation (TCM), the technique used in telephone-line modems to squeeze high spectral efficiency out of 3 kHz-bandwidth analog telephone lines.
- Computer storage devices such as hard disk drives.
References[edit]
- ^Stefan Host, Rolf Johannesson, Dmitrij K. Zigangirod, Kamil Sh. Zigangirod, and Viktor V. Zyablod.'On the Distribution of the Output Error Burst Lengths for Viterbi Decoding of Convolutional Codes'.
- ^Curry, S. J.; Harmon, W. D.'A bound on Viterbi decoder error burst length'.
External links[edit]
Wikimedia Commons has media related to Viterbi coding. - Forney, G. David, Jr (29 Apr 2005). 'The Viterbi Algorithm: A Personal History'. arXiv:cs/0504020.
- Details on Viterbi decoding, as well as a bibliography.
- Viterbi algorithm explanation with the focus on hardware implementation issues.
- r=1/6 k=15 coding for the Cassini mission to Saturn.
- Online Generator of optimized software Viterbi decoders (GPL).
- GPL Viterbi decoder software for four standard codes.
- Description of a k=24 Viterbi decoder, believed to be the largest ever in practical use.
- Generic Viterbi decoder hardware (GPL).
Retrieved from 'https://en.wikipedia.org/w/index.php?title=Viterbi_decoder&oldid=944278176'...">Viterbi Algorithm Ppt For Mac(15.04.2020) - meaning000strongest0001relatively strong0010relatively weak0011weakest0100weakest1101relatively weak1110relatively strong1111strongest1
Of course, it is not the only way to encode reliability data.
The squaredEuclidean distance is used as a metric for soft decision decoders.
Path metric unit (PMU)[edit]
A sample implementation of a path metric unit for a specific K=4 decoderA path metric unit summarizes branch metrics to get metrics for paths, where K is the constraint length of the code, one of which can eventually be chosen as optimal. Every clock it makes decisions, throwing off wittingly nonoptimal paths. The results of these decisions are written to the memory of a traceback unit.
The core elements of a PMU are ACS (Add-Compare-Select) units. The way in which they are connected between themselves is defined by a specific code's trellis diagram.
Since branch metrics are always , there must be an additional circuit (not shown on the image) preventing metric counters from overflow. An alternate method that eliminates the need to monitor the path metric growth is to allow the path metrics to 'roll over'; to use this method it is necessary to make sure the path metric accumulators contain enough bits to prevent the 'best' and 'worst' values from coming within 2(n-1) of each other. The compare circuit is essentially unchanged.
A sample implementation of an ACS unitIt is possible to monitor the noise level on the incoming bit stream by monitoring the rate of growth of the 'best' path metric. A simpler way to do this is to monitor a single location or 'state' and watch it pass 'upward' through say four discrete levels within the range of the accumulator. As it passes upward through each of these thresholds, a counter is incremented that reflects the 'noise' present on the incoming signal.
Traceback unit (TBU)[edit]
A sample implementation of a traceback unitBack-trace unit restores an (almost) maximum-likelihood path from the decisions made by PMU. Since it does it in inverse direction, a viterbi decoder comprises a FILO (first-in-last-out) buffer to reconstruct a correct order.
Note that the implementation shown on the image requires double frequency. There are some tricks that eliminate this requirement.
Implementation issues[edit]
Quantization for soft decision decoding[edit]
In order to fully exploit benefits of soft decision decoding, one needs to quantize the input signal properly. The optimal quantization zone width is defined by the following formula:
where is a noise power spectral density, and k is a number of bits for soft decision.
Euclidean metric computation[edit]
The squared norm () distance between the received and the actual symbols in the code alphabet may be further simplified into a linear sum/difference form, which makes it less computationally intensive.
Consider a 1/2 convolutional coder, which generates 2 bits (00, 01, 10 or 11) for every input bit (1 or 0). These Return-to-Zero signals are translated into a Non-Return-to-Zero form shown alongside.

D = ( v r → − v i → ) 2 = v r → 2 − 2 v r → v i → + v i → 2 Each square term is a normed distance, depicting the energy of the symbol. For ex., the energy of the symbol vi = {±1, ±1} may be computed as
Thus, the energy term of all symbols in the code alphabet is constant (at (normalized) value 2).
The Add-Compare-Select (ACS) operation compares the metric distance between the received symbol vr and any 2 symbols in the code alphabet whose paths merge at a node in the corresponding trellis, vi(0) and vi(1). This is equivalent to comparing
and
But, from above we know that the energy of vi is constant (equal to (normalized) value of 2), and the energy of vr is the same in both cases. This reduces the comparison to a minima function between the 2 (middle) dot product terms,
since a min operation on negative numbers may be interpreted as an equivalent max operation on positive quantities.
Each dot product term may be expanded as
where, the signs of each term depend on symbols, vi(0) and vi(1), being compared. Thus, the squared Euclidean metric distance calculation to compute the branch metric may be performed with a simple add/subtract operation.
Traceback[edit]
The general approach to traceback is to accumulate path metrics for up to five times the constraint length (5 (K - 1)), find the node with the largest accumulated cost, and begin traceback from this node.
However, computing the node which has accumulated the largest cost (either the largest or smallest integral path metric) involves finding the maxima or minima of several (usually 2K-1) numbers, which may be time consuming when implemented on embedded hardware systems.
Most communication systems employ Viterbi decoding involving data packets of fixed sizes, with a fixed bit/byte pattern either at the beginning or/and at the end of the data packet. By using the known bit/byte pattern as reference, the start node may be set to a fixed value, thereby obtaining a perfect Maximum Likelihood Path during traceback.
Limitations[edit]
A physical implementation of a viterbi decoder will not yield an exact maximum-likelihood stream due to quantization of the input signal, branch and path metrics, and finite traceback length. Practical implementations do approach within 1dB of the ideal.
The output of a Viterbi decoder, when decoding a message damaged by an additive gaussian channel, has errors grouped in error bursts.[1][2]Single-error-correcting codes alone can't correct such bursts, so either the convolutional code and the Viterbi decoder must be designed powerful enough to drive down errors to an acceptable rate, or burst error-correcting codes must be used.

Punctured codes[edit]
A hardware viterbi decoder of punctured codes is commonly implemented in such a way:
- A depuncturer, which transforms the input stream into the stream which looks like an original (non punctured) stream with ERASE marks at the places where bits were erased.
- A basic viterbi decoder understanding these ERASE marks (that is, not using them for branch metric calculation).
Software implementation[edit]
One of the most time-consuming operations is an ACS butterfly, which is usually implemented using an assembly language and appropriate instruction set extensions (such as SSE2) to speed up the decoding time.
Applications[edit]
The Viterbi decoding algorithm is widely used in the following areas:
- Radio communication: digital TV (ATSC, QAM, DVB-T, etc.), radio relay, satellite communications, PSK31 digital mode for amateur radio.
- Decoding trellis-coded modulation (TCM), the technique used in telephone-line modems to squeeze high spectral efficiency out of 3 kHz-bandwidth analog telephone lines.
- Computer storage devices such as hard disk drives.
References[edit]
- ^Stefan Host, Rolf Johannesson, Dmitrij K. Zigangirod, Kamil Sh. Zigangirod, and Viktor V. Zyablod.'On the Distribution of the Output Error Burst Lengths for Viterbi Decoding of Convolutional Codes'.
- ^Curry, S. J.; Harmon, W. D.'A bound on Viterbi decoder error burst length'.
External links[edit]
Wikimedia Commons has media related to Viterbi coding. - Forney, G. David, Jr (29 Apr 2005). 'The Viterbi Algorithm: A Personal History'. arXiv:cs/0504020.
- Details on Viterbi decoding, as well as a bibliography.
- Viterbi algorithm explanation with the focus on hardware implementation issues.
- r=1/6 k=15 coding for the Cassini mission to Saturn.
- Online Generator of optimized software Viterbi decoders (GPL).
- GPL Viterbi decoder software for four standard codes.
- Description of a k=24 Viterbi decoder, believed to be the largest ever in practical use.
- Generic Viterbi decoder hardware (GPL).
Retrieved from 'https://en.wikipedia.org/w/index.php?title=Viterbi_decoder&oldid=944278176'...">Viterbi Algorithm Ppt For Mac(15.04.2020)